As promised in Part 2 of this series, in this third installment, I’ll continue to wade into the choppy waters of string current. This is of such importance in any NAND Flash, and especially in the vertical channel 3D NAND Flash approach championed by Samsung and Toshiba that I’ll spend some time describing what it is.
Now there is a small coterie that knows everything about this subject, but they are usually associated with the 5 permanent members of the “NAND Flash Security Council” (namely Samsung, Toshiba, Hynix, Micron and SanDisk). This is not for them but for interested spectators who want to learn more.
A good analogy usually helps in understanding and keeps the subject from becoming arcane and complex. Let’s extend the ice skating analogy from the previous post. Don’t worry if you can’t skate. You would just be the equivalent of an electron in a very disordered material!
Before you, the electron, try to race along the NAND string channel, let’s “walk” along to inspect the course. We’ll make it even more difficult to get to the other end by throwing in obstacles along the path.
The first such obstacle will be a drawbridge. You need to be able to skate across this. If it’s up, you’re stuck and will have to wait until it lowers. This is of course the analogy for the channel region controlled by the gate. One small but important problem with this bridge (only for this analogy you understand) is that the mechanical joints are a bit rusty, with the nasty consequence that it is left in a partial “up-state” each time it is opened and closed. In addition, its remnant “up-ness” increases as it is used more often. In other words, it gets increasingly difficult to skate across when it is supposed to be down. (The usefulness of this contrived analogy will soon become apparent so stay with me here!)
OK, now you’ve managed to skate across that drawbridge only to find another one, identical to the first, a short way further along the channel of ice. Get across this one and there’s another, and another, and yet another. And so it goes on until you’ve crossed 24 of them all in a straight line.
Now go back to the beginning of this skating channel and imagine standing, as an electron, with your skates glinting in the freezing winter’s sun, looking far off into the distance towards the 24th drawbridge. You’re one of a whole crowd of skating electrons that will make the trip when the starter’s pistol fires. This will be a skating marathon!
Let’s now link this analogy to a NAND channel. Each drawbridge is a channel region controlled by a gate. The number of drawbridges along this icy course is the number of cells in a NAND string. Samsung’s V-NAND has 24 drawbridges while the most advanced 2D NANDs have 128. The crystalline versus disordered channel I’ll come to later with some additions to the skating marathon analogy.
Figure 1 shows a generic vertical channel 3D NAND on its side showing 4 channels and 8 gates. You, the skating electron, will pick one channel and try to skate all the way through the “icy” course making your way across the drawbridges when you can.
What would a stored memory-state-one look like? Remember, this is when you (the skating electron) can get across the drawbridge. You guessed it. The drawbridge would be down and you would be able to skate easily across. And a stored memory-state-zero? Simple. The drawbridge would be up and you would be stuck on one side trying to keep warm.
Now imagine your buddy at the other end of this icy NAND string course. He’s being paid to write down the memory state of each NAND cell. Unfortunately he has no skates and needs you to skate to the respective drawbridge, find out, and then try to skate to him to tell him. He radios to you to inspect drawbridge number 11 for example.
Of course each cell in a NAND string is either in a memory-state-one or a zero. So there may be drawbridges leading up to number 11 that are in the up-state. This also goes for the bridges leading from number 11 all the way to your buddy standing at the end of the course. How do you tell him the state of bridge 11?
Here’s where we talk about “passing”, which is where all bridges leading up to bridge 11 and from bridge 11 to the end are forced into a down state. This is done no matter what state each bridge is storing. Your buddy can operate the levers to do this. Therefore, if he sees you appear at the end of the icy course (steamy breath clouding your face), he knows that bridge 11 must be in a down state. If he doesn’t see you appear at all, he knows that bridge 11 must be up with you stuck on one side of it (no doubt cursing your luck since your buddy has a nice, warm cup of soup for you).
So there we have it. Your buddy radios to you the bridge number to inspect. You see all the other bridges being lowered into a passing state. You start skating to the bridge to be inspected. And then you either stop if it’s in the up state or you continue on across it in its down state and meet your buddy at the end of the icy NAND string course.
Perfect? Well not really. And here is where it starts to get nice and interesting. It turns out those drawbridges have some defects that impede your path.
The first is that the bridges in the up state don’t really come all the way down when put in the passing state. Instead, they end up in a sort of half-way up half-way down state that forces you to clamber over them to get through. Anyone who has skated knows how difficult it is to skate uphill! The bridges that are down are still easy to skate across.
The second, already mentioned above, is that forcing the bridges into a passing state leaves them in a partial “up-state” each time they are opened and closed. In addition, their “up-ness” increases as they are used more often. The bridges that were originally down change faster into this partial up-state. The greater the mechanical force used to get all those bridges to pass and help you on your trip, the faster is the change into a partial up-state. So if your buddy wants to make it easy for you on your first marathon trip by really forcing those gates down, the more difficult he is making it for any subsequent trip along the same skating course. Also, you may be confused when you are asked to inspect a certain bridge that had been in the down-state at the beginning but has moved into an up-state with all that forced passing.
With this drawbridge analogy in mind, we are now ready to define two key parameters and an important concept for any NAND string.
Imagine all bridges are in the down-state in addition to the one that you are asked to inspect by your buddy. He then applies the mechanical force to allow you to pass (since he doesn’t know what state each bridge is in). You then skate easily all the way along the course and arrive at the other end fairly quickly after your buddy had fired the starting pistol.
This is equivalent to the best-case NAND string current where all cells are in the memory-state-one, including the one that is being inspected (in other words, read). Electrons flow easily along this channel which means relatively high current.
Now let’s have all the bridges in the up-state except for the one you are asked to inspect which is in the down-state. Your buddy forces all those up-state bridges into a passing down-state. But we have already seen that there is a defect that means they end up being in a partial up-state. You hear the starter pistol and start clambering over all those partial up-state passing bridges. By the time you reach your buddy, you are sweating and exhausted having taken much more time to get to him compared to the best case NAND string current case.
This is equivalent to the worst-case NAND string current where all cells are in the memory-state-zero except for the one being inspected. Electrons flow with difficulty along this channel which means relatively low current.
The key concept has to do with the second defect mentioned above, namely pass disturb. We have seen how your buddy can make it easier for you to skate the course by extra forcing of the passing bridges into the down-state. The cost of doing this is that these bridges end up being bent into a partial up-state for the next time you need to skate across them.
The NAND string current can be increased by ratcheting up the voltage on the gates that are being used to pass. This is especially important in the worst-case string current situation. Otherwise, it may be so small to be lost in the noise and be mistaken for no current at all.
Why not just keep going up in pass gate voltage to maximize the string current? Well, this leads to pass disturbs of these cells and results in a gradual change of their memory state, not to mention a further gradual decline in the string current. This is the same as your buddy applying extra force on the pass bridges to make it easy for you to get through but at the cost of leaving them in a partial up-state.
What values of current are to be expected from regular 2D crystalline channel NAND? In the case of such 2D crystalline channels, these are published now and again. After much digging, I found a recent publication where both the best and worst case string currents were given for a 64-cell NAND string. The best case was 1700 nanoAmps while the worst case was 80 nanoAmps. See the effect of those up-state drawbridges forced into a down-state – a 20-times reduction in NAND string current going from best case to worst case!
Now let’s turn our attention to those vertical 3D NAND strings. Remember that the channel is not single crystal but has a polycrystalline disordered grain structure. What does that do to our analogy?
As in the previous post, imagine now that the drawbridges all stretch across the ravines and rough ice of a glacier. When your buddy radios to you which bridge to inspect, you see the passing bridges lowered and then you can stumble along the path slowly. Now you get the picture – smaller currents compared to crystalline channels.
As I said before, the big companies working in this area usually avoid stating the absolute values of the string currents, especially the worst case version and especially for polycrystalline channels. Wouldn’t it be nice to get real experimentally derived numbers and see how they compare with the crystalline 2D NAND strings?
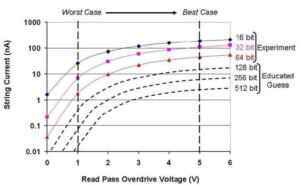
It turns out my company, Schiltron, has made strings of devices that can be made, through electrical connections, to behave just like 3D NAND strings with polycrystalline channels. If you want to dig into the details, there is a white paper that covers this. For those who just want the results, have a look at Figure 2, which shows the 3D NAND string currents on the Y-axis and what is called the read pass overdrive voltage on the X-axis. This voltage is just equivalent to the amount of forcing that your buddy exerts on the passing drawbridges. The greater the force (voltage), the easier it is (more current) for you to get through the icy course.
Notice a few things in Figure 2. The Y-axis is on a log-scale. Curves are given for different string lengths, from 16 cells to 512 cells. Remember, Samsung’s V-NAND is initially 24 cells and so between the 16 and 32-cell curves. Also, notice two vertical lines given for the best case and worst case string currents.
Now you can see that the vertical channel 3D NAND manufacturers must be getting a best case string current of about 100 nanoAmps and a worst case string current of about 10 nanoAmps for a 24-cell long string. Remember that a nanoAmp is one billionth of an Amp. These are whopping reductions from the crystalline case given above where these numbers were 1700 nanoAmps and 80 nanoAmps respectively, and for 64 cells to boot! We’re talking about a 10-times reduction in currents from the crystalline case.
This is not the only thing to take away from figure 2. Remember that vertical channel 3D NAND can only go up to increase single chip memory capacities. In other words, the strings have to get longer. Look what happens to those string currents. The next generation capacity numbers (48 cells instead of 24 cells) would be about 50 nanoAmps (best) and 2 nanoAmps (worst). Then the one after that (96 cells high) would give about 15 nanoAmps (best) and 0.6 nanoAmps (worst). These numbers do not bode well for any technology that claims to be anything other than a “flash in the pan” (pun intended).
The astute among you may say “why not just increase the forcing on the passing drawbridges?” In other words, increase the read pass overdrive voltage in figure 2. Remember what happens in our analogy? Those over-forced bridges end up in a partial up-state.
It turns out that any NAND string (2D and 3D) that relies on a Charge Trap approach (see my first post), as these vertical channel approaches most certainly do, is more prone to this pass disturb effect than existing tried-and-trusted 2D approaches which use a floating gate approach. So, just when we need to overdrive to maximize the string currents in disordered channels, we are constrained by this nasty effect. Attempting to minimize it has the troublesome consequence of dramatically ramping up the voltages needed to program and erase each cell. This pass disturb is another strategic item usually not mentioned by the manufacturers.
Again, I am not bound by such bonds of secrecy and can give real experimental data on what happens. But this juicy data can wait until the next post! ~ AJW
