The mid-1920’s were the miracle years for quantum mechanics. The “Old Quantum Theory” originating with Niels Bohr, had reached crisis point by the end of 1924. Wave-particle duality from Einstein and de Broglie called for something new.
The great theorists, Heisenberg, Born, Jordan, Schrödinger, and Dirac, published different formulations of a new theory that were quickly shown to be equivalent descriptions of quantum mechanics. It did not take long before this new theory was being used to explain unusual phenomena.
“Among all the successes of quantum mechanics as it evolved in the third decade of the 20th century, none was more impressive than the understanding of the tunnel effect”. So wrote E. Merzbacher in 2002.
“Though I speak with the mathematical tongues of men and of angels, and have not physical intuition, I am become as sounding brass, or a tinkling cymbal,” with apologies to St. Paul.
A graphical method works wonders to develop a physical intuition for quantum mechanical tunneling. An excellent book for this is “Elementary Quantum Mechanics” by Ronald Gurney who was one of the first to apply the new mechanics and specifically tunneling to radioactive nuclear disintegration.
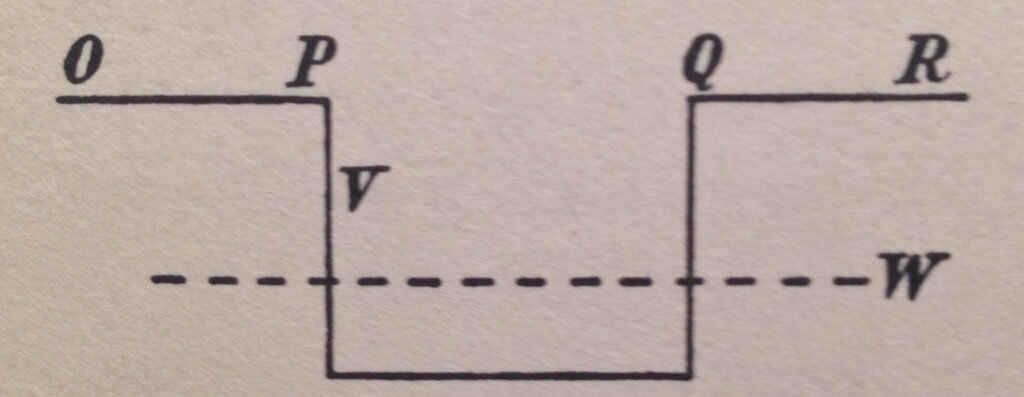
Figure 1 shows a particle confined to a potential energy bucket where its total energy W is less than the potential energy V at the top of the bucket walls but greater than the potential energy within the bucket. The horizontal direction shows the position and the vertical direction of the energy.
In the new mechanics, de Broglie had proposed that particles have wave properties. Schrödinger thus came out with his wave equation after being encouraged by P. Debye. In Gurney’s marvelous description, “Schrödinger hit on the idea that an equation whose solutions are de Broglie waves where W > V might also give reasonable results where W < V”. Figure 2 shows his equation.
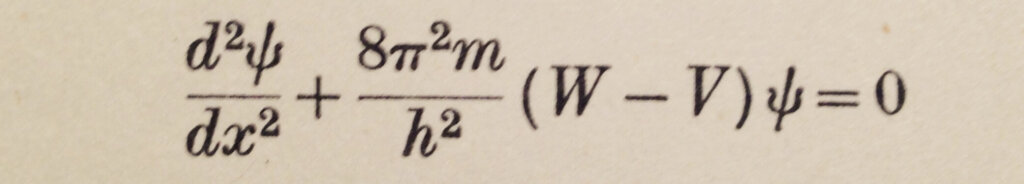
The “thing” that “waves” and is a solution of Schrödinger’s equation is called ψ (“psi” in Greek). Although the wave equation came from Schrödinger, the correct interpretation of ψ came from Born.
It turns out that ψ² is proportional to the probability of finding the particle at any particular position in space. This then connects the strangeness of quantum mechanics to actual experimental measurements.
A possible Schrödinger wave pattern solution (time-independent for the purists) for the particle with energy W in the potential energy bucket of Figure 1 is shown in Figure 3. ψ is the wave function pattern while ψ² is the square of its value.
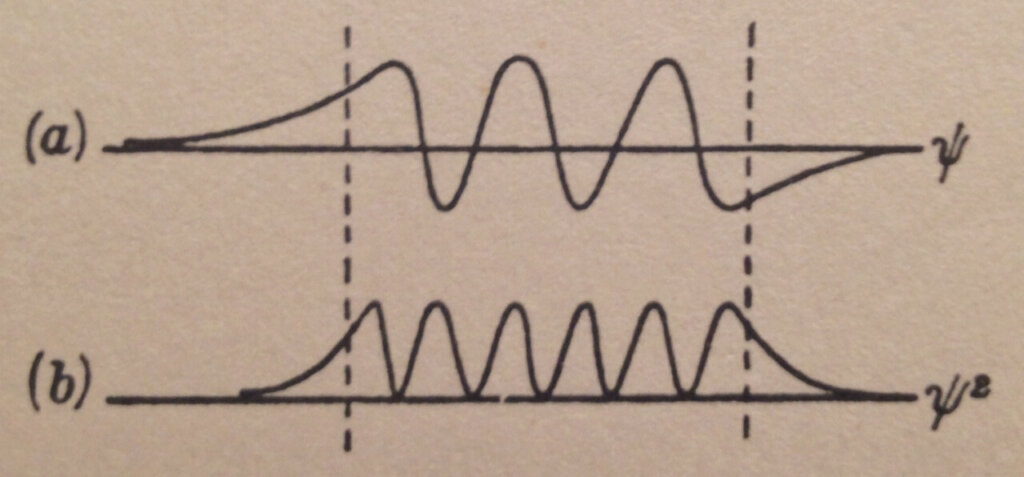
In general, the wave function ψ is a complex number and ψ² is the square of its modulus which is a real number. In our simplified analysis, following Gurney’s approach, we treat the wave function as a real number too.
Notice in Figure 3 ψ² is not zero outside the potential energy bucket but rather decays exponentially towards zero as we get further from the bucket.
Let’s take a closer look at that in Figure 4.
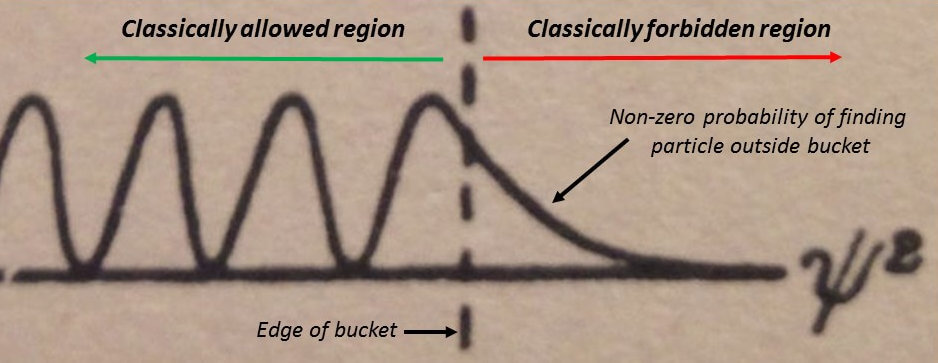
In other words, quantum mechanics allows a particle to move through a barrier.
As Gurney writes, “the classical division into allowed and forbidden regions disappears”.
The barriers in Figure 1 beyond Q to the right and beyond P to the left stretch to infinity. The probability of finding the particle quickly dies off outside the classically allowed regions as seen in Figure 4. These barriers have become “fuzzy” and “diffuse” rather than sharp.
Understanding tunneling is but a small step from where we are now.
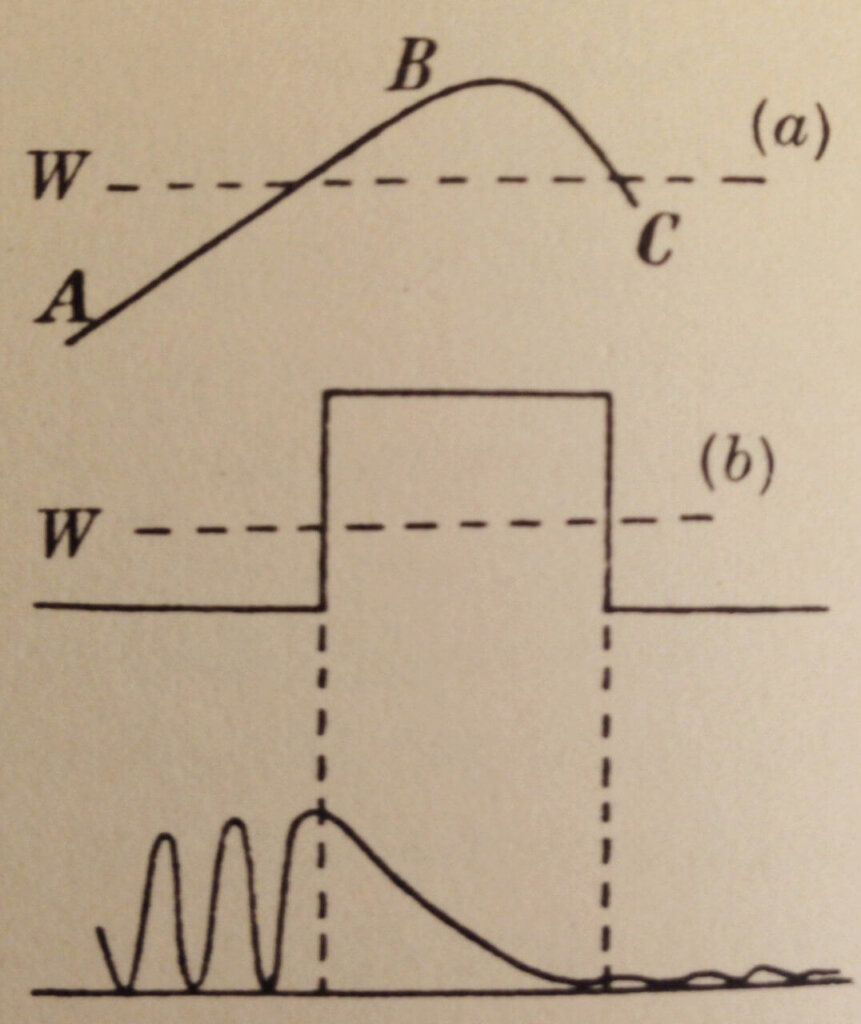
Figure 5 shows how a particle can quantum mechanically tunnel through a barrier that classically it could never get through. The barrier is thin enough such that the exponential decay of ψ² within the barrier has not reached zero. The particle starts out on the left-hand side (large amplitude ψ² = high probability of finding it here). The barrier exponentially reduces the amplitude but the particle is found on the right-hand side (small amplitude ψ² = low probability of finding it here).
And that’s tunneling.
One of the first applications of quantum mechanical tunneling and one that we shall return to later as it applies to silicon memory devices was in the emission of electrons from metals in intense electric fields. Two famous physicists worked on this topic in 1928, Ralph Fowler (Lord Rutherford’s son-in-law) and Lothar Nordheim.

Figure 6 shows extracts from the Fowler-Nordheim paper from 1928. Their Figure 1 (i) shows an electron in a metal approaching the edge of the metal and finding a potential energy barrier. This is similar to our Figure 1 above. Without any external electric field, this barrier goes on to infinity and, as we have seen in our Figures 3 and 4, the probability of finding the electron outside the metal rapidly decays towards zero.
However, Fowler-Nordheim’s Figure 1 (ii) shows what happens to the potential energy curve when an external electric field is applied. Suddenly we get a triangular barrier where the width of the barrier for any electron is dependent on the strength of the field. Stronger fields result in narrower barriers which mean a higher probability of tunneling out.
One of the most famous applications of tunneling and indeed the first time quantum mechanics was applied to the atomic nucleus was for α-particle nuclear disintegration.

Ronald Gurney and Edward Condon, almost simultaneously with George Gamov, explained the strange behavior of α-particle nuclear disintegration by solving Schrödinger’s wave equation with a potential energy curve given in Figure 7.
The α-particle has a total energy given by the height of DF above the X-axis. We have seen that possible wave patterns can leak through the barrier at DB and FH. The higher the energy of the α-particle, the narrower is the barrier and the more likely the particle will tunnel out.
Many other diverse phenomena have been shown to be driven by quantum mechanical tunneling. Both Longair’s book and Merzbacher’s article provide fascinating background on these.
For our story, we must move forward to the 1960’s and the rise of silicon-based microelectronics, in part 2 of this series.



















